Net Present Value, Duration, and CAPM in Light of Investment Theory: A Comment on Kruk
Abstract: In her paper “Corporate Risk Evaluation in the Context of Austrian Business Cycle Theory” recently published in this journal, Joanna Kruk aims to investigate how artificially low interest rates resulting from central bank intervention distort individual investment appraisals and ultimately result in both entrepreneurial misjudgment and resource-wasting malinvestment, fueling the business cycle. She identifies entrepreneurs’ net present value calculations, supposedly unadjusted for risk, as a major issue and suggests adjusting those calculations for risk via both the duration method and the Capital Asset Pricing Model to mitigate the distorting effects. Her argumentation is, however, trapped in neoclassical reasoning and is adversely affected by several misconceptions of the net present value criterion. This comment seeks to reveal those fallacies and explain how to address uncertainty when using net present value calculations to make those calculations part of the solution rather than part of the problem of entrepreneurial misjudgment. The findings are derived from German investment theory rooted in the Austrian school of thought, meaning that they differ compared to those of neoclassical finance theory.
JEL Classification: B31, B41, B53, G32
Thomas Hering (hering@fernuni-hagen.de) is a professor of business economics and holds the Chair of Investment Theory and Business Valuation at Fern-University in Hagen, Germany. Michael Olbrich (olbrich@iwp.uni-saarland.de) is a professor of business economics and chair of the Institute of Auditing at Saarland University, Saarbrücken, Germany. David J. Rapp (david.rapp@imt-bs.eu) is an associate professor of accounting and management control at Institut Mines-Télécom Business School and member of the research lab LITEM, Univ. Paris-Saclay, Univ. Evry, IMT-BS, Evry/Paris, France.
INTRODUCTION
In her paper “Corporate Risk Evaluation in the Context of Austrian Business Cycle Theory” recently published in this journal, Kruk (2020) seeks to explain why and how artificially low interest rates brought about by central bank intervention distort individual investment appraisals and eventually lead to clustered entrepreneurial misjudgment, malinvestment, and capital consumption, that is, the business cycle. Her perception of previous research is that “little attention was paid to the analysis of corporate finance and the causes of companies’ erroneous decisions about initiating and carrying out unprofitable undertakings,” which indicates she believes that investigating “the motivation of financial decisions on a micro-level can shed new light on the foundations of the emergence of the business cycle” (Kruk 2020, 131–32). Certainly economic calculation in general, and entrepreneurial investment decisions in particular, are yet to be thoroughly explored from the perspective of the acting individual and those areas should be stringently investigated owing to their significance for both Austrian theorizing (e.g., Austrian business cycle theory [ABCT]) and practice. However, there has already been far more discussion on the topic than Kruk (2020) suggests, both in general terms and with explicit links to ABCT.1
In essence, Kruk (2020) asserts that the economy shifts toward a riskier position in response to artificially low interest rates and that decision-makers fail to incorporate that risk appropriately in their investment calculi. By neglecting investment risk, entrepreneurs invest in projects that are only seemingly profitable. To aid in mitigating this issue, Kruk suggests adjusting net present value (NPV) calculations, which serve as the basis of investment decisions, for risk. Kruk’s underlying idea is to decrease resulting NPVs by applying mathematical adjustments to make investment projects look less feasible in order to deter entrepreneurs from making poor investments. Specifically, Kruk suggests NPVs risk-adjusted based on both duration and the Capital Asset Pricing Model (CAPM).
However, entrepreneurs calculating an NPV must consider their individual circumstances if they are to receive a figure that is realistically supportive of the decision-making process, and naturally, this includes the consideration of what Kruk labels risk. Mises (1952, 126, italics added) explains:
One of the items of a bill of costs is the establishment of the difference between the price paid for the acquisition of what is commonly called durable production equipment and its present value. This present value is the money equivalent of the contribution this equipment will make to future earnings. There is no certainty about the future state of the market and about the height of these earnings. They can only be determined by a speculative anticipation on the part of the entrepreneur.
Contrary to Kruk’s reasoning, neither duration nor CAPM serves to support entrepreneurs’ speculative decision-making well. This comment aims to uncover the misconceptions inherent in Kruk’s argument and to present alternative ways of addressing uncertainty when using the NPV as a tool to support entrepreneurial decision-making. To do so, we build on Prussian-German business economics, especially investment theory, which has been developed in the German-speaking world based on Austrian economics (Schmalenbach 1919, 334; Mises 1933, 9; [1960] 2003, 226; Schmidt 1933, 106; Herbener and Rapp 2016, 13; Olbrich, Rapp, and Follert 2020) and which fully adopts the perspective of the acting individual rather than building on the well-known escapist assumptions of neoclassicism.
RISK, UNCERTAINTY, AND INVESTMENT DECISIONS
Kruk’s (2020, 138) diagnosis is that “wealth maximizing investors are evaluating projects only using risk-free NPV [and that, hence,] they may underestimate the risk associated with their investment decisions.” That is why “we cannot exclude risk from its role in the profitability of the investment projects, and this factor should be included in further analysis” (Kruk 2020, 137).
However, rather than failing to take account of the “risks” associated with a particular investment, investors largely do attempt to consider them in their investment calculi. Kruk (2020, 145–46) herself emphasizes that not only academics but also investment practitioners by and large rely on the CAPM, which is believed to provide a reasonable risk-adjusted discount rate for NPV considerations. In other words: the problem Kruk seemingly identified is a mere straw man and the solution she proposes in response to it exactly corresponds to how most decision-makers already decide on their investments. Nevertheless, the issues of entrepreneurial misjudgment and malinvestment have not been mitigated, let alone resolved. Hence, adjusting NPV calculations for “risk” via the CAPM will evidently not offer a means to reduce clustered entrepreneurial malinvestment. Rapp (2015) indicates that neoclassical models such as the CAPM are part of the problem rather than the solution. In particular, they fuel the business cycle due to their strong interdependence with market data.
Kruk, moreover, is mistaken when associating regular entrepreneurial investment decisions with risk. Rather than probabilistic, calculable risk, it is Knightian uncertainty (Knight 1921) that gives rise to entrepreneurship (Mises 1949) and, hence, entrepreneurial decision problems in the first place. Kruk conveys the impression that entrepreneurial decision problems could—with some assumptions (146, 147) here and there—be solved mathematically. However, in the presence of Knightian uncertainty, decision problems are not well-structured and optimal solutions out of reach (Wilson and Alexis 1962; Adam and Witte 1979; Adam 1983; 1996; Rapp and Olbrich 2020) of even the most elaborate math. Rather, entrepreneurs (must) imagine how the future might look and apply judgment to ultimately make their (investment) decisions (Klein 2008; Foss and Klein 2012; Packard, Clark, and Klein 2017). Such judgment can certainly be informed by genuine economic calculation; given they are unrelated to the real world, however, models springing from neoclassicism, in particular the CAPM, are beyond the scope of any toolbox reasonably applicable for that purpose (Olbrich, Quill, and Rapp 2015; Follert et al. 2018).
ON COMBINING NPV, DURATION, AND CAPM
Duration describes the sensitivity of the price of a security to changes in the interest rate in the case of a flat interest rate structure. In a perfect capital market under certainty, the price corresponds to the NPV of the future earnings2 and the duration equals the absolute amount of the interest (factor) elasticity of the price. Duration can be interpreted as an “average capital commitment period,” too, which reflects the average time at which one unit of the NPV flows to the investor (Matschke, Hering, and Klingelhöfer 2002, 173–75; Kruk 2020, 138–39).
A stream of future earnings with a low ratio is interpreted as less “risky” than one with a higher ratio, since the investor is interested in the earliest possible return on his initial investment. In this respect, the duration does indeed contain some information related to the uncertainty of future earnings.
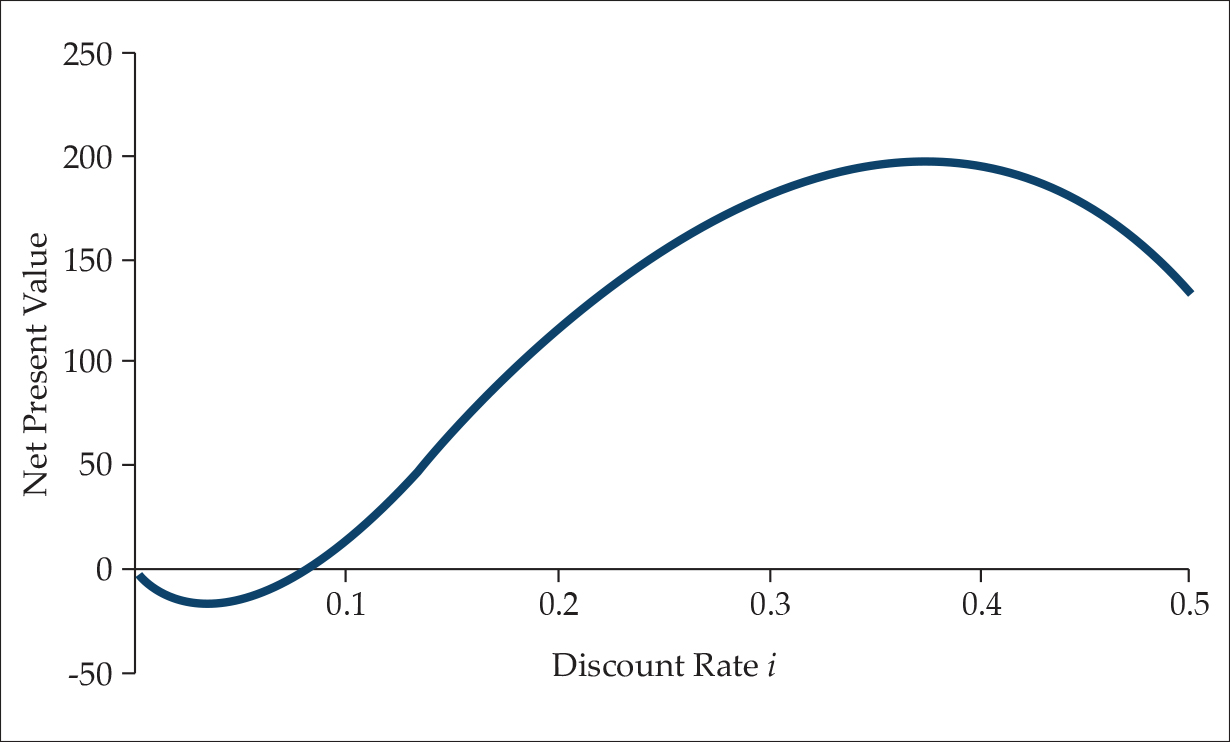
However, the informational value of this key figure is clearly limited. In contrast to investments in traded securities, entrepreneurial ventures usually require investments in tangible assets. In such cases, however, a negative correlation between the interest rate and NPV is anything but a given. Referring to Rothbard (1962 [2009], 62–63), Kruk (2020, 135–38) too assumes a decreasing NPV when interest rates rise. A simple example reveals, however, that this assumption need not be met: Suppose a business in the field of large-scale plant construction accepts a considerable early customer down payment, which leads to the following expected future income stream (–$19,000, $69,000, –$80,000, $28,000, $2,000). The resulting NPV curve of this project is shown in Figure 1 (Hering 2017, 294–95):
Figure 1. Interest rate impact on NPV in our example (Hering 2017, 295)
If the current interest rate is 10 percent, for example, an expected rise in the interest rate does not result in a decreased NPV and, hence, less willingness to invest on the part of the entrepreneur; instead, an increased NPV makes the project appear more attractive than previously. This simple yet realistic example alone shows how an artificial and arbitrary manipulation of the relevant discount rate (which should actually be determined by the entrepreneur’s time preference) intended to reduce NPVs and, thus, decision-makers’ willingness to invest, ultimately fails to do so. Despite this, Kruk (2020, 145–47) recommends discounting with an interest rate adjusted for a risk premium via the CAPM.
Kruk (2020, 139) is correct to point out that the duration estimates NPV reactions to the change in interest rates proportionally. It thus commits an estimation error owing to the relationship being nonlinear. Therefore, the larger the interest rate change, the less is its explanatory power. Additionally and above all, the duration suffers from the unrealistic assumption of a steady interest rate (both before and after the interest rate change) in all periods (Matschke, Hering, and Klingelhöfer 2002, 175). In reality, that is, in imperfect capital markets, such flat interest rate structures are merely rare exceptions rather than standard occurrences.
While the informational value of duration is in itself fairly limited and essentially confined to theoretical borderline cases, linking it to the finance theory-based CAPM as suggested by Kruk (2020, 145–48) worsens matters. In contrast to both NPV and duration, which are decision models, the CAPM is a neoclassical equilibrium model initially established to explain particular market outcomes ex post. For that reason alone, it is entirely pointless for decision-making purposes from an ex ante perspective (Hering 2017, 303–10; 2021, 236–40); the CAPM was simply not designed to support entrepreneurial decision-making (yet has been largely unsuccessful in fulfilling its intended purpose too; hence, it has failed miserably on all counts). Kruk (2020, 145–46) points to CAPM’s popularity among both practitioners and academic proponents of finance theory to justify recourse to it; however, no matter how popular the CAPM has been, that popularity cannot overcome the fundamental issues associated with the model’s application in investment appraisal.
The linking of NPV, duration, and CAPM suffers from another logical flaw: while both NPV and duration are multi-period models, that is, they (in most cases) cover more than one time period and can often span decades, the standard CAPM as described and recommended by Kruk (2020,146) is limited to the consideration of just a single period. In other words: Kruk suggests using a risk-adjusted discount rate derived from a static one-period equilibrium model for the appraisal of uncertain multi-period investment projects in the real world, that is, in dynamic disequilibrium.
HOW TO ACCOUNT FOR UNCERTAINTY IN INVESTMENT APPRAISAL
Preparing for investment decisions by acting as if a future state of affairs were fully knowable seems decidedly inappropriate. We thus wholeheartedly agree with Kruk (2020, 146, 148) that (reasonably) considering the uncertainty associated with investment projects in NPV (or duration) calculi can contribute to the entrepreneur’s Verstehen and, thereby, inform his ultimate judgment. Knightian uncertainty neither allows for exact calculations of NPVs in terms of point values nor seemingly definite decision suggestions. The best investment appraisal can do to support entrepreneurs in their decision-making under conditions of uncertainty is to reveal the financial consequences of the range of uncertain future states of affairs imagined by the entrepreneur. Therefore, methods transparently uncovering the uncertainty associated with investment projects, as suggested by proponents of investment theory, rather than hiding uncertainty’s implications in condensed point values, as suggested by neoclassical finance theory, best serve decision-making (Hering 2017, 273–75; Olbrich, Quill, and Rapp 2015, 25–27; Herbener and Rapp 2016, 19–20). Sensitivity analyses and simulations are particularly suitable methods to support the entrepreneur. Figure 2 shows an example (Hering 2017, 334–53) resulting from one such analysis based on a Monte Carlo simulation (Hertz 1964; Coenenberg 1970), which compares NPV distributions of two investment alternatives (A1, A2) given individual entrepreneurial estimations of both future earnings and period-specific discount rates.
Figure 2. Comparison of two simulated NPV distributions (Hering, Schneider, and Toll 2011, 424)
In contrast to the risk premium concept, which manipulates NPV calculi on the level of the input data and immediately presents a seemingly certain point value (Kruk 2020, 147–48), a simulative approach to considering uncertainty in investment appraisal calculates and visualizes the financial consequences of thousands and thousands of combinations of future earnings and discount rates based on the entrepreneur’s estimate, illustrating the possible outcomes of each alternative path of action and thus providing a transparent basis for decision-making. Whether, as figure 2 suggests at least at first glance, alternative A1 should actually be preferred over A2 on the basis of its profile being located somewhat further to the right cannot be decided upon in general terms; instead it ultimately remains an entrepreneurial decision under uncertainty demanding judgment. Needless to say, the entrepreneur may complement the quantitative results provided by investment appraisal with qualitative, non-calculable considerations when formulating his final decision (Herbener and Rapp 2016, 20; Hering 2017, 398–400; Hering 2021, 40–45).
CONCLUSION
Neoclassical finance theory follows a (seemingly) objective, market value-based concept and hence, in some sense, resembles “the naive conception of the layman that things have value in themselves, i.e., intrinsic value” (Ritenour 2016, 192). Considering uncertainty in investment appraisal on the basis of escapist models derived from that theory, and particularly the CAPM, therefore cannot support acting humans making investment decisions in the real world. It would be more productive to apply scenario analyses (Hering 2017, 359, 375) and simulations to reveal the possible effects of uncertainty on future states of affairs in imperfect capital markets based on individual entrepreneurial imagination. Doing so would offer entrepreneurs the most transparent source to inform their judgment. The final decision to invest, however, certainly remains a purely entrepreneurial one that eludes mathematical formulation (Hering 2021, 12–13, 44–45, Herbener and Rapp, 2016, 20).
Applying models derived from neoclassical finance theory to support investment appraisal fuels the business cycle. Entrepreneurial evaluations based on actual individual circumstances and estimations of the future (taking into account subjective assessments of the stage of the business cycle) seem superior both on an individual level and in terms of the ability to mitigate the issue of clustered malinvestment as a whole. Although that approach cannot resolve the underlying problem of distorted interest rates and market prices initiated by central bank intervention, it can at least limit its effects (Rapp 2015).
1. See, in particular, Rapp (2015); Olbrich, Quill, and Rapp (2015); Herbener and Rapp (2016); Olbrich, Rapp, and Venitz (2016); Rapp, Olbrich, and Venitz (2017); Follert et al. (2018); Rapp, Olbrich, and Venitz (2018); Olbrich, Rapp, and Follert (2020).
2. We deliberately choose not to apply the term “cash flow” used by proponents of finance theory to describe the numerator in NPV analysis. Proponents of investment theory, as well as Mises (1952, 126), speak of “future earnings,” “future benefits,” or “future income” instead and emphasize the numerator’s subjective nature. “Future benefits must be forecasted from the perspective of the person who is valuing and choosing. Predictions of future benefits depend upon personal factors, such as the dividend policy, individual tax rates including potential tax loss carry-forwards, and individual synergies” (Herbener and Rapp 2016, 16). The importance of synergies in particular for entrepreneurial success has been intensively discussed within the Austrian school; see, e.g., Lachmann (1956, 13), Cwik (2008, 66), Klein (2010, 110), Boettke and Piano (2019, 22).



